CS基地班 1.计算机基础知识

数据的定义：数据是指所有能输入到计算机并被计算机程序处理的符号的总称，是用于输入电子计算机进行处理，具有一定意义的数字、字母、符号和模拟量等的统称。

一、数值信息在计算机的表示

二进制：只用0和1两个符号，一般以八位（1字节）出现。

十进制：0～9。

八进制：0～7，人为规定以0开头的数字为八进制。

十六进制：0～9，A、B、C、D、E、F，人为规定以0x开头。

1. 十进制转换为二进制数

1. 将十进制整数除以2，得到商和余数。
2. 将商继续除以2，得到新的商和余数。
3. 重复步骤2，直到商为0。
4. 将得到的所有余数从下往上依次排列，即为对应的二进制数。

示例：将十进制数13转换为二进制

1
2
3
4

13 ÷ 2 = 6 余 1
6 ÷ 2 = 3 余 0
3 ÷ 2 = 1 余 1
1 ÷ 2 = 0 余 1

从下往上读取余数，得到二进制数1101。

因此，十进制数13的二进制表示为1101。

[!Warning]
注意需要补全至八位：00001101

2. 十进制小数转换为二进制数

对于十进制小数转换为二进制数，我们主要关注小数部分的转换。方法如下：

1. 将小数部分乘以2。
2. 取出整数部分（0或1）作为二进制小数的一位。
3. 将小数部分再次乘以2。
4. 重复步骤2和3，直到小数部分为0或达到所需精度。

示例：将十进制小数0.625转换为二进制

1
2
3

0.625 × 2 = 1.25  取整数部分1
0.25 × 2 = 0.5    取整数部分0
0.5 × 2 = 1.0     取整数部分1

因此，十进制小数0.625的二进制表示为0.101。

注意：某些十进制小数在二进制中可能是无限循环小数，这种情况下需要根据实际需求截断精度。

3. 几种进制之间的转换

二进制转换为十进制

二、原码、反码、补码

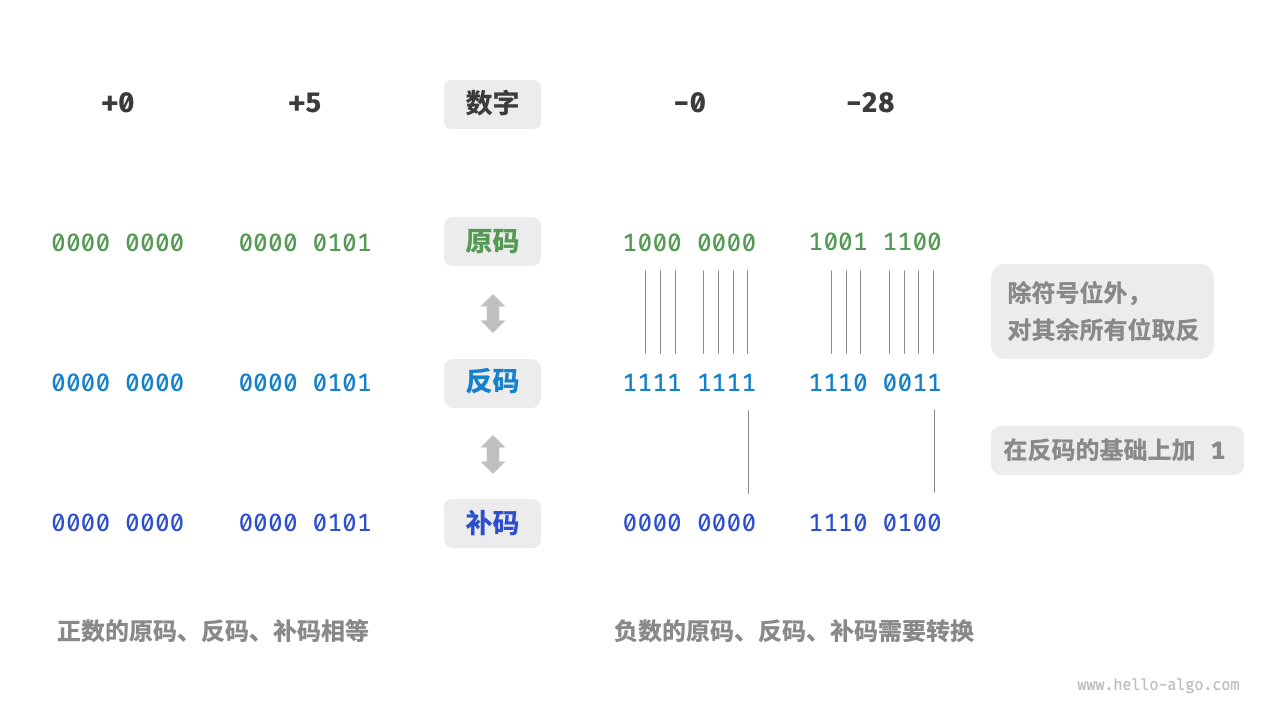
机器数

最高位为符号位。（0=正数，1=负数）

原来的数值称为机器数的真值。

1
2

+3[原] = 00000011
-3[原] = 10000011

原码

机器数本身。

反码

对于正数：反码与原码相同。

对于负数：反码保持原码符号位不变，其他各位取反数。

1
2

+3 = 00000011[原码] = 00000011[反码]
-3 = 10000011[原码] = 11111100[反码]

补码

正数：原码。

负数：反码+1。

1
2

+3[补] = 00000011[原] = 00000011[反] = 00000011[补]
-3[反] = 10000011[原] = 11111100[反] = 11111101[补]

参考内容

https://higoge.github.io/2015/07/02/basic03/

三、字符

(一) 西文字符（ASCII）

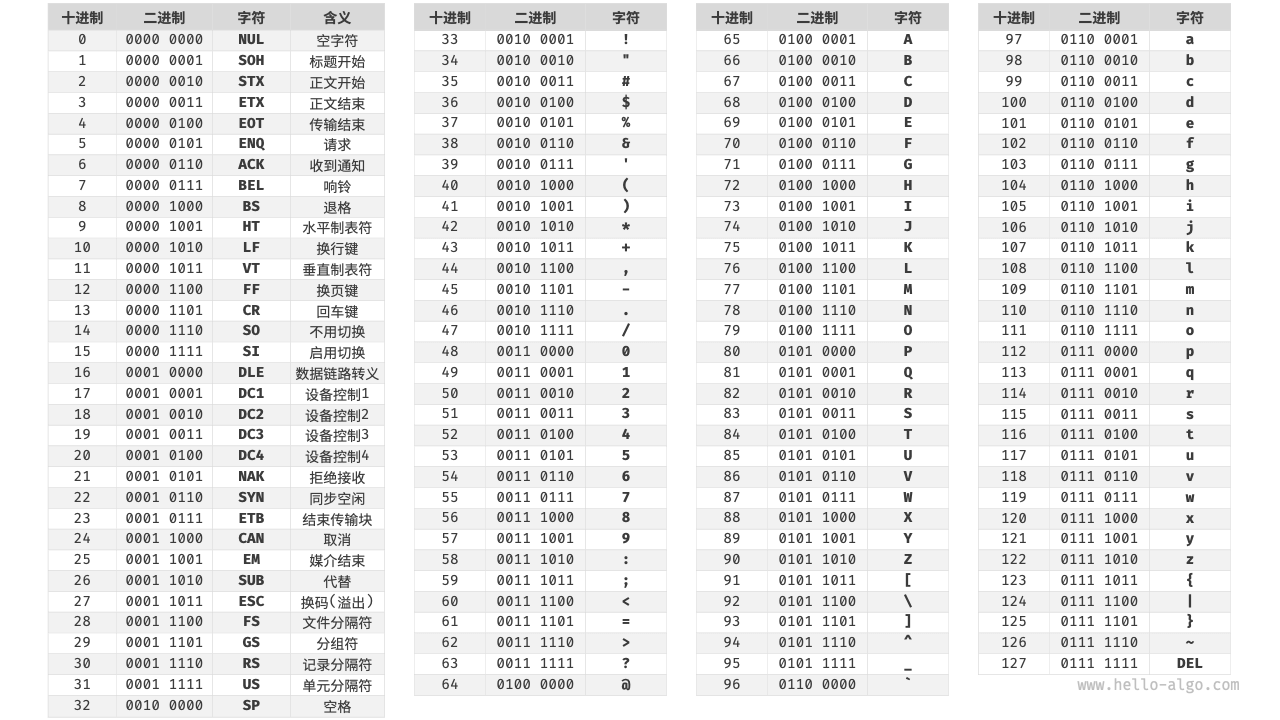
特点：

• 二进制编码为7位。
• 有128种不同的字符编码。
• 一个ASSCII码占用一个字节（8个bit）

ASCII中特殊的编码

(二) 汉字字符

• 每个汉字在计算机中都有一个二进制代码。
• 每个汉字的二进制代码为两个字节（16个bit），称为机内码。

四、扩展

(一) 比特和字节

Bit，比特，也叫二进制位，是信息的最小单位。一个比特可以理解为一个开关量，0就是关，1就是开。

Byte，字节，由8个Bit组成。它通常用作计算机信息计量单位。字节在一些规范中称作Octet。

Bit简写为b，Byte简写为B。