数据结构的基本概念、数据的存储结构和逻辑结构、集合、线性结构、树形结构、图型结构的构成方式、顺序存储和链式存储的区别与联系、线性表的使用方法与运算过程、栈和队列使用方法与运算过程

基本概念

数据

数据是描述客观事物的物理符号，是所有能输入到计算机中并被计算机程序加工处理的符号的总称。如数值、字符、文字等。数据是信息的载体。

数据元素

数据元素是数据处理的基本单位。

数据项

数据项是具有独立意义的最小数据单位。

[!example]
📚 举个图书馆的例子：

1 2 3 4 5 6 7 8 9 10

图书馆（数据） ├── 《哈利波特》（数据元素） │ ├── 书名：哈利波特（数据项） │ ├── 作者：J.K.罗琳（数据项） │ └── ISBN：123456（数据项） ├── 《小王子》（数据元素） │ ├── 书名：小王子（数据项） │ ├── 作者：圣埃克苏佩里（数据项） │ └── ISBN：789012（数据项） └── ...其他书籍

🔍 概念解析：

1. 数据（Data）：整个图书馆的所有书籍信息
2. 数据元素（Data Element）：每一本单独的书籍（数据中的基本单位）
3. 数据项（Data Item）：书籍的具体属性（书名/作者等）

🎯 关键区别：

• 数据项是数据的原子单位（不可再分）
• 数据元素 = 多个数据项的集合
• 数据 = 多个数据元素的集合

💡 另一个比喻：
数据就像整个Excel表格
↓
每行数据（数据元素）就是一个学生的完整信息
↓
每个单元格（数据项）就是姓名/学号等具体信息

📊 层级关系图示：

1 2 3 4 5

数据（整个表） ↓ 数据元素（一行记录） ↓ 数据项（单个单元格）

结构

被计算机加工的各数据元素之间不是孤立的，彼此间存在某种关系。

数据结构

数据结构是带有结构特性的数据关系的集合。

[!example]
📦 生活中的「结构」
假设你开了一个快递驿站，你可能会用以下方式整理包裹：

1 2 3 4

结构（抽象的组织思路） ├─ 方案1：包裹随便堆在地上（无结构） ├─ 方案2：按取件码顺序排列（有序结构） └─ 方案3：将包裹分区域存放（分区结构）

结构 是一种 抽象的组织思路，没有具体的操作规则，只描述如何安排物品的关系。

---

🖥️ 计算机中的「数据结构」
当你要用程序实现快递站的包裹管理，就需要具体的 数据结构：

1 2 3 4

数据结构（具体的组织规则 + 操作方法） ├─ 用「队列」实现：先到的包裹先被取走（FIFO） ├─ 用「栈」实现：后到的包裹先被取走（LIFO） └─ 用「哈希表」实现：通过取件码直接找到包裹（快速定位）

数据结构 = 结构（组织方式） + 操作规则（增删改查），它像一套完整的操作说明书。

---

🖼️ 图例对比

1 2 3 4 5 6 7 8 9 10 11

快递站结构（抽象思路） │ ▼ 按取件码顺序排列（有序结构） │ ▼ 用「数组」实现 → 数据结构1 （连续内存存储，通过下标快速访问） │ 用「链表」实现 → 数据结构2 （分散存储，通过指针连接包裹）

• 结构 是蓝图（比如”按顺序排列”）
• 数据结构 是具体施工方案（比如用数组或链表实现）

---

🌰 举个栗子：排队取快递
2. 结构要求：先到的客户先取件（排队规则）
3. 数据结构选择：

• 用 队列（先进先出）→ 符合结构要求 ✅
• 若错误地用 栈（后进先出）→ 违背结构要求 ❌

---

🔑 关键总结

	结构（Structure）	数据结构（Data Structure）
层级	抽象概念（要做什么）	具体实现（怎么做）
内容	只描述数据之间的关系	包含存储方式 + 操作算法
类比	建筑的设计图纸	施工方案（材料+建造步骤）

通过这种对比，你就能理解为什么学习数据结构时，总是从「逻辑结构」和「物理结构」两个角度分析了！(•̀ω•́)✧

逻辑结构

指数据集合中各数据元素之间所固有的逻辑关系。

• 集合：结构中的数据元素之间除了“同属于一个集合”的关系外，别无其他关系。集合是元素关系极为松散的一种结构。
• 线形结构：一对一
• 树形结构：一对多
• 图状或网状结构：多对多

在数组和链表中，数据按照一定顺序排列，体现了数据之间的线性关系；而在树中，数据从顶部向下按层次排列，表现出“祖先”与“后代”之间的派生关系；图则由节点和边构成，反映了复杂的网络关系。

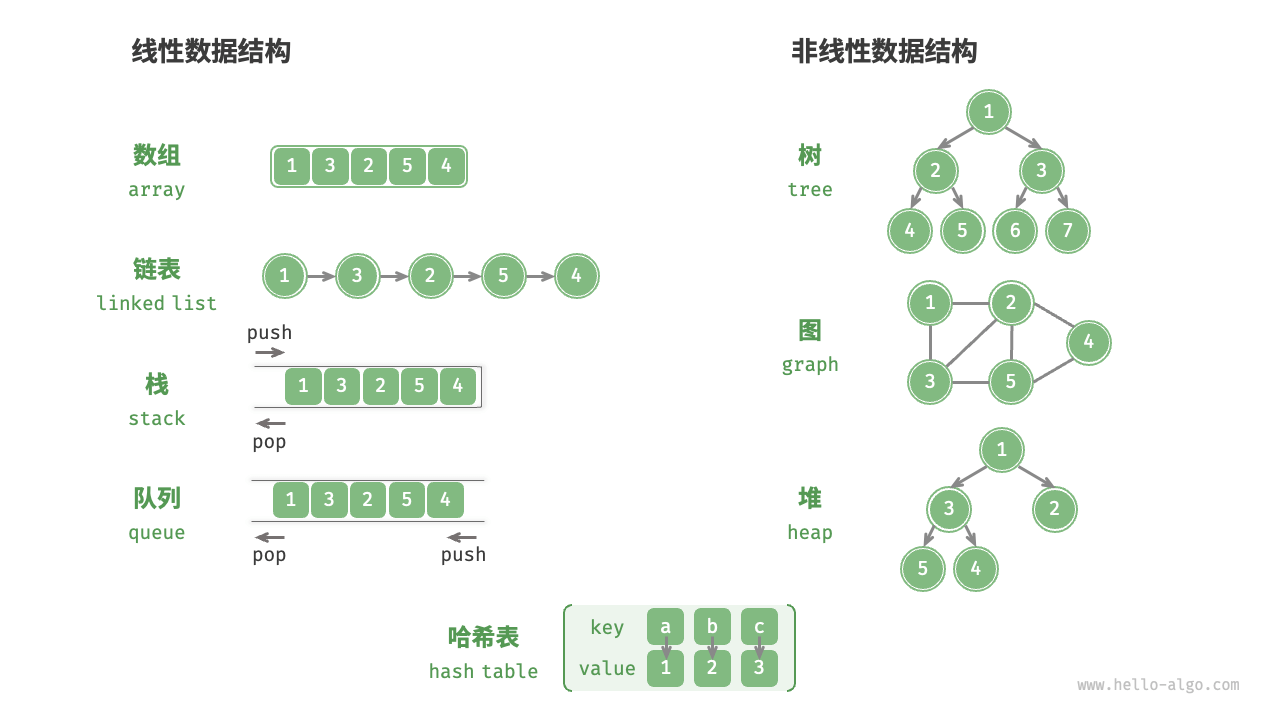
如图 3-1 所示，逻辑结构可分为“线性”和“非线性”两大类。线性结构比较直观，指数据在逻辑关系上呈线性排列；非线性结构则相反，呈非线性排列。

• 线性数据结构：数组、链表、栈、队列、哈希表，元素之间是一对一的顺序关系。
• 非线性数据结构：树、堆、图、哈希表。

非线性数据结构可以进一步划分为树形结构和网状结构。

• 树形结构：树、堆、哈希表，元素之间是一对多的关系。
• 网状结构：图，元素之间是多对多的关系。

存储结构

又称为 数据的物理结构。

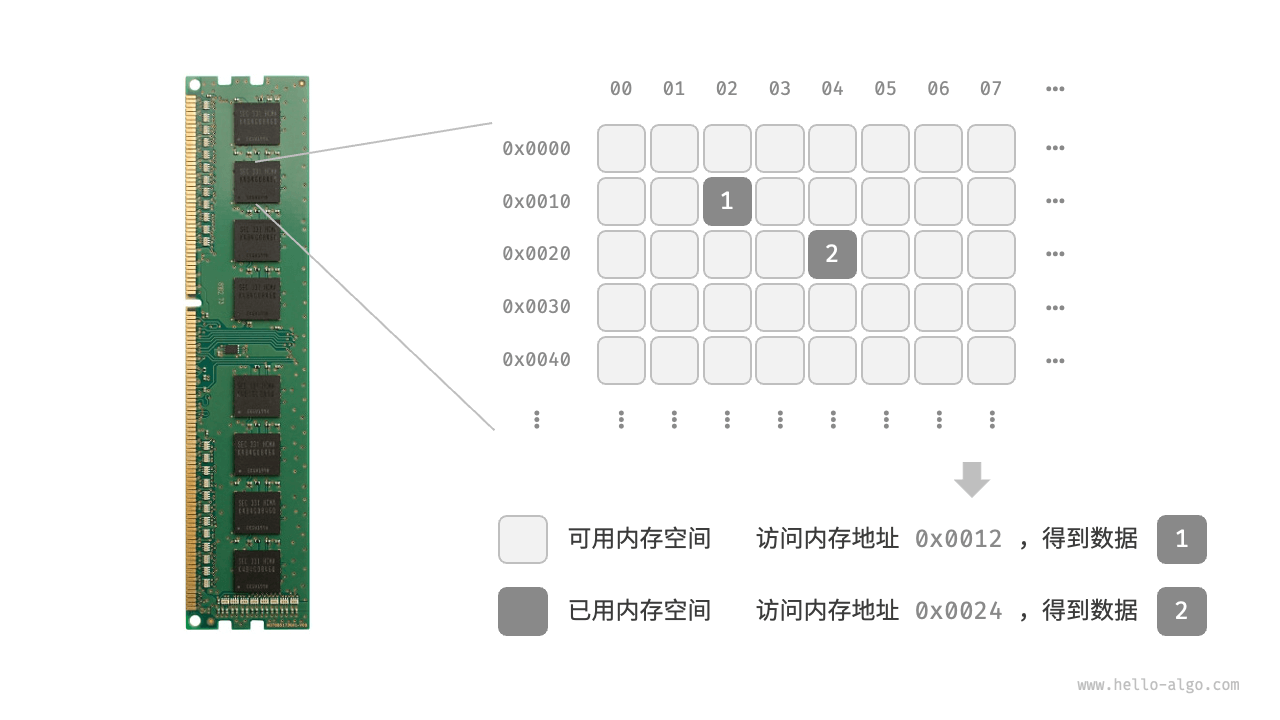
当算法程序运行时，正在处理的数据主要存储在内存中。图 3-2 展示了一个计算机内存条，其中每个黑色方块都包含一块内存空间。我们可以将内存想象成一个巨大的 Excel 表格，其中每个单元格都可以存储一定大小的数据。

系统通过内存地址来访问目标位置的数据。如图 3-2 所示，计算机根据特定规则为表格中的每个单元格分配编号，确保每个内存空间都有唯一的内存地址。有了这些地址，程序便可以访问内存中的数据。

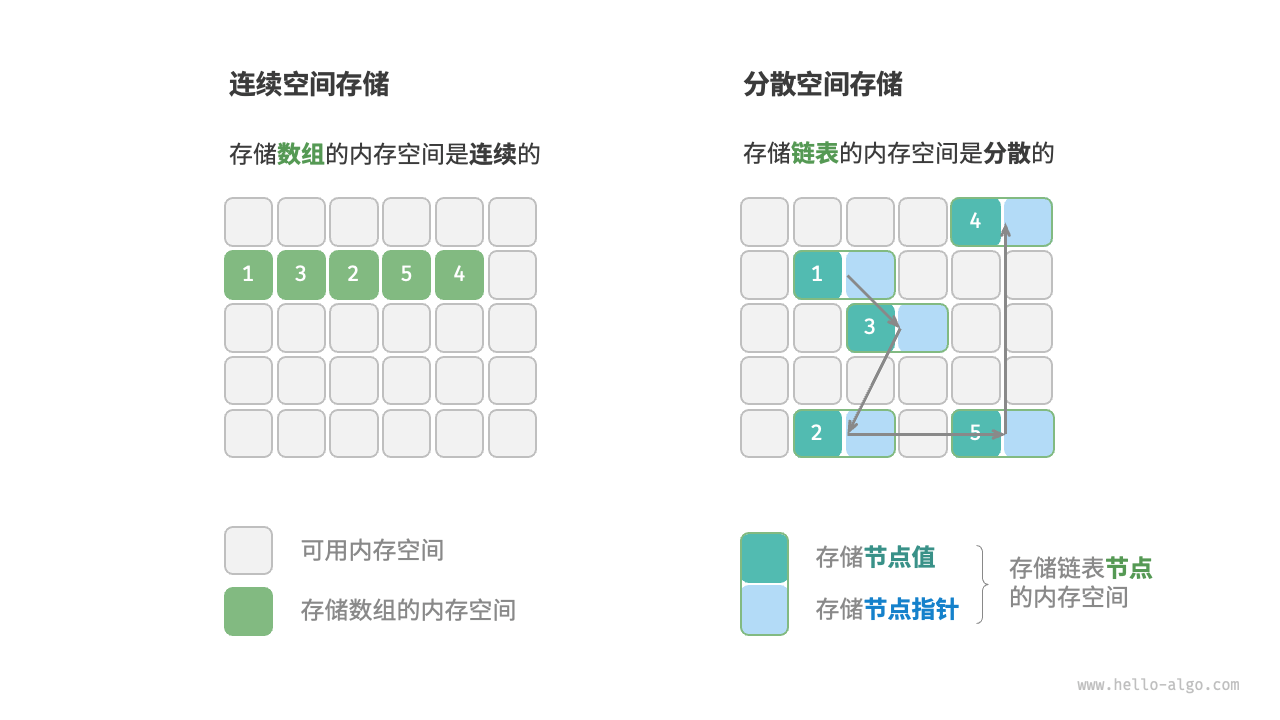
如图 3-3 所示，物理结构反映了数据在计算机内存中的存储方式，可分为连续空间存储（数组）和分散空间存储（链表）。物理结构从底层决定了数据的访问、更新、增删等操作方法，两种物理结构在时间效率和空间效率方面呈现出互补的特点。

顺序结构

特点：

• 存储密度大，存储空间利用率高
• 插入、删除运算不便，会引起大量节点的移动。

链式结构

• 借用指针来实现

特点：

• 存储密度小，存储空间利用率低
• 逻辑上相邻的节点物理上不必相邻，可用于线性表、树、图等多种逻辑结构的存储表示。
• 插入、删除操作灵活方便，不必移动节点，只需要改变节点中的指针值即可。

值得说明的是，所有数据结构都是基于数组、链表或二者的组合实现的。例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表。

• 基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。
• 基于链表可实现：栈、队列、哈希表、树、堆、图等。

线性表

最简单、最常用的一种数据结构。
逻辑结构：线性结构

顺序表

又称”一维数组”。

• 采用顺序存储结构的线性表。
• 各种高级语言里的一维数组就是用顺序方式存储的线性表。
  特点：
• 表中各数据元素在存储空间中是按逻辑顺序依次存放的。
• 表中所有元素所占的存储空间是连续的。

[!tip]

• 查找一个元素是方便的。
• 插入、删除运算不方便，会导致大量节点的移动。

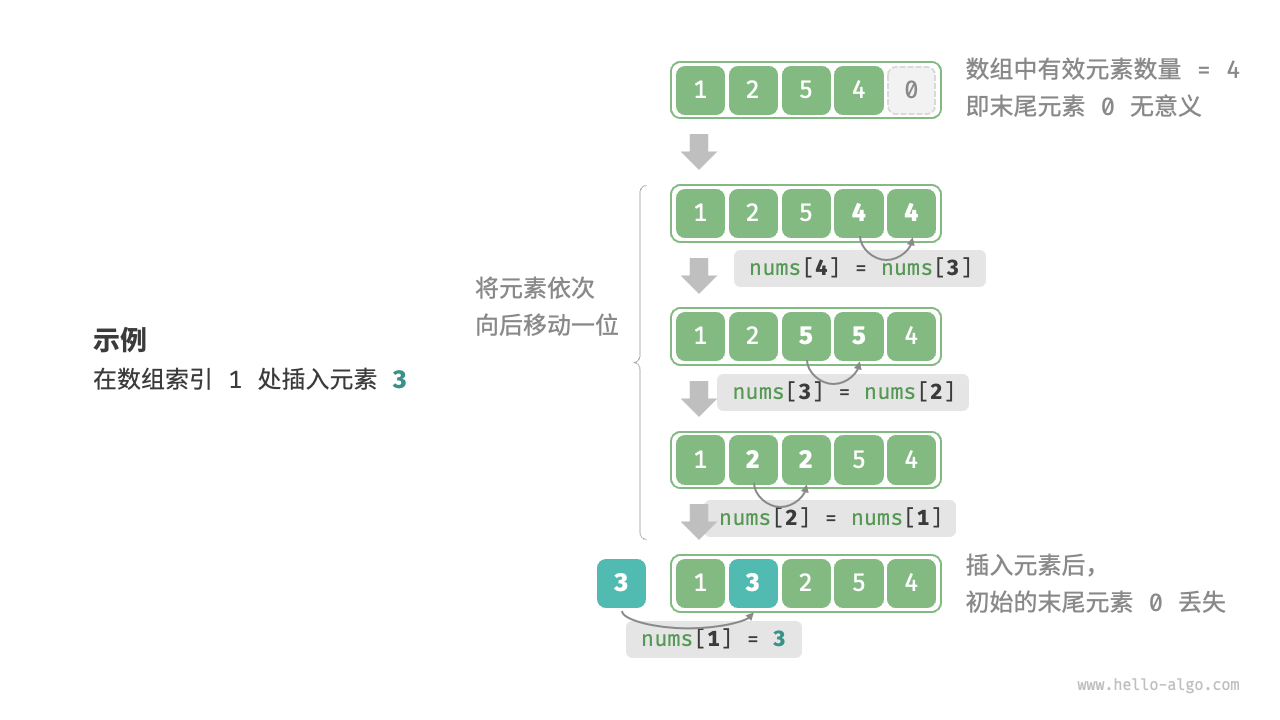
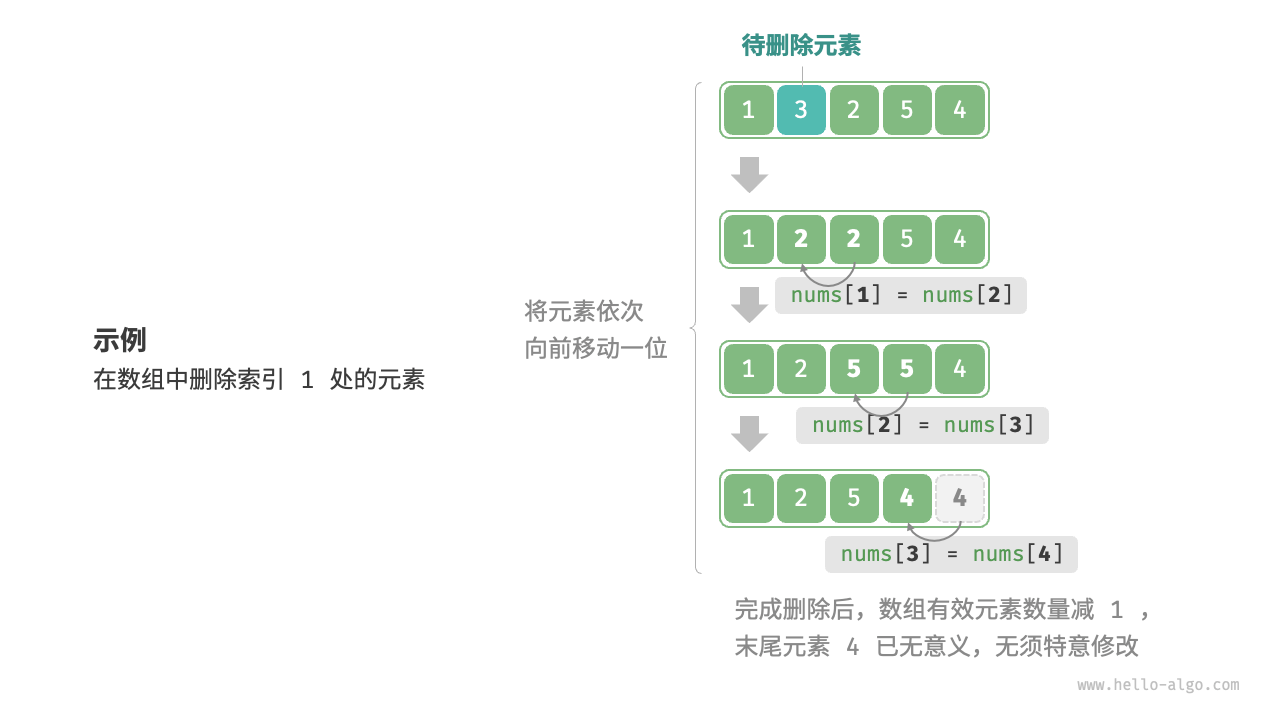
插入与删除

[!tip]

• 插入一个节点平均需要移动的节点个数为$\frac{n}{2}$，算法的时间复杂度是$O(n)$
• 删除一个节点平均需要移动的节点个数为$\frac{n-1}{2}$，算法的时间复杂度是$O(n)$

链表

采用链式存储结构的线性表。

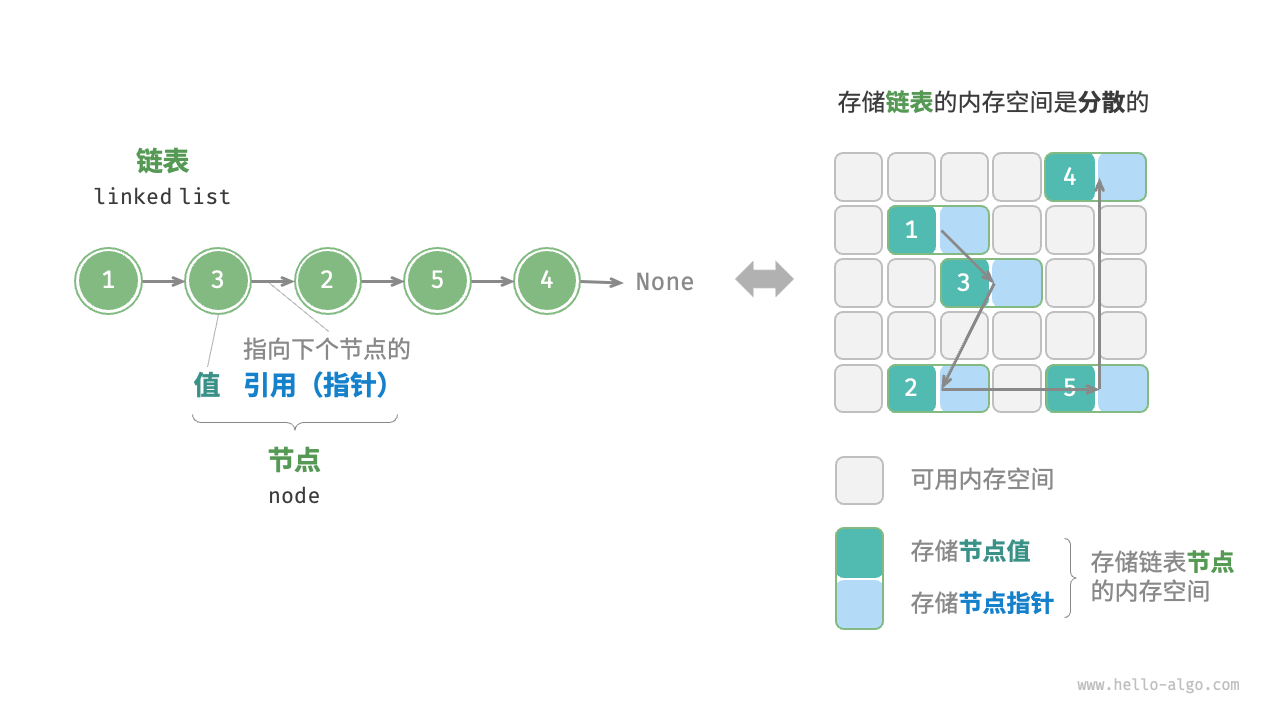
观察图 4-5 ，链表的组成单位是节点（node）对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。

• 链表的首个节点被称为“头节点”，最后一个节点被称为“尾节点”。
• 尾节点指向的是“空”，它在 Java、C++ 和 Python 中分别被记为 null、nullptr 和 None

插入与删除

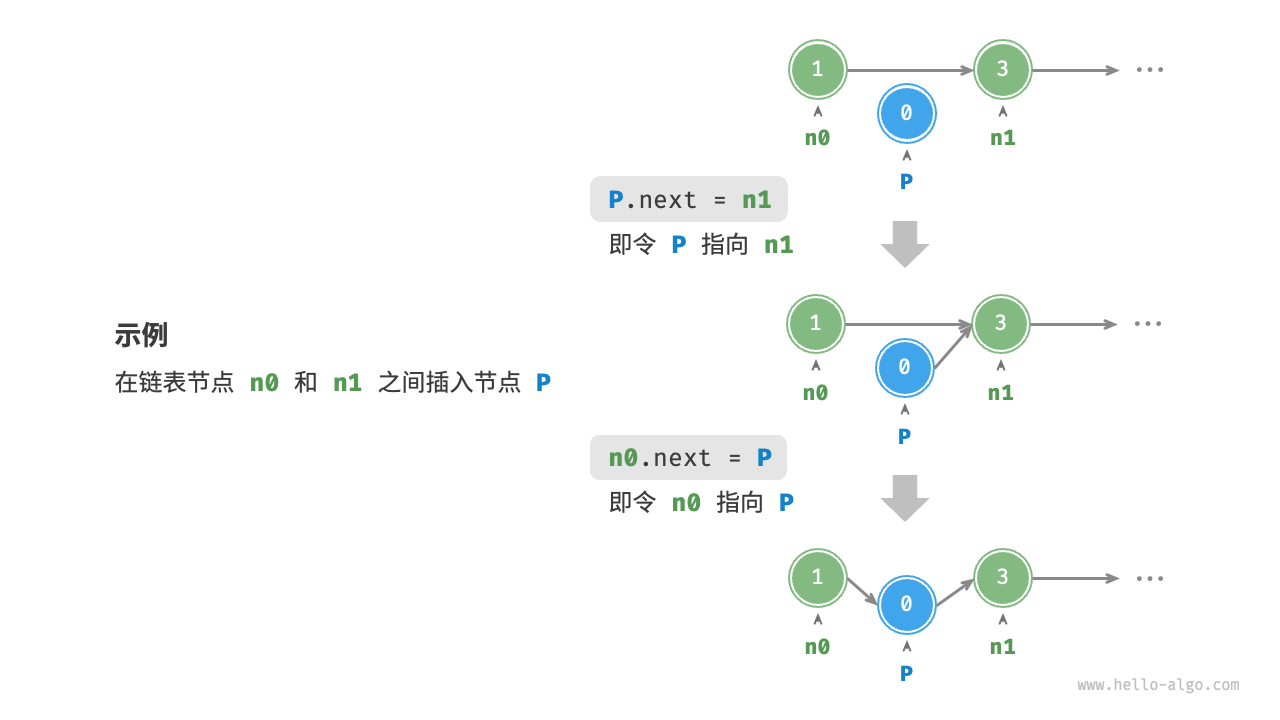
在链表中插入节点非常容易。如图 4-6 所示，假设我们想在相邻的两个节点 n0 和 n1 之间插入一个新节点 P ，则只需改变两个节点引用（指针）即可，时间复杂度为 $O(1)$ 。

相比之下，在数组中插入元素的时间复杂度为 $O(n)$ ，在大数据量下的效率较低。

[!tip]
此处书上称”指针域”。

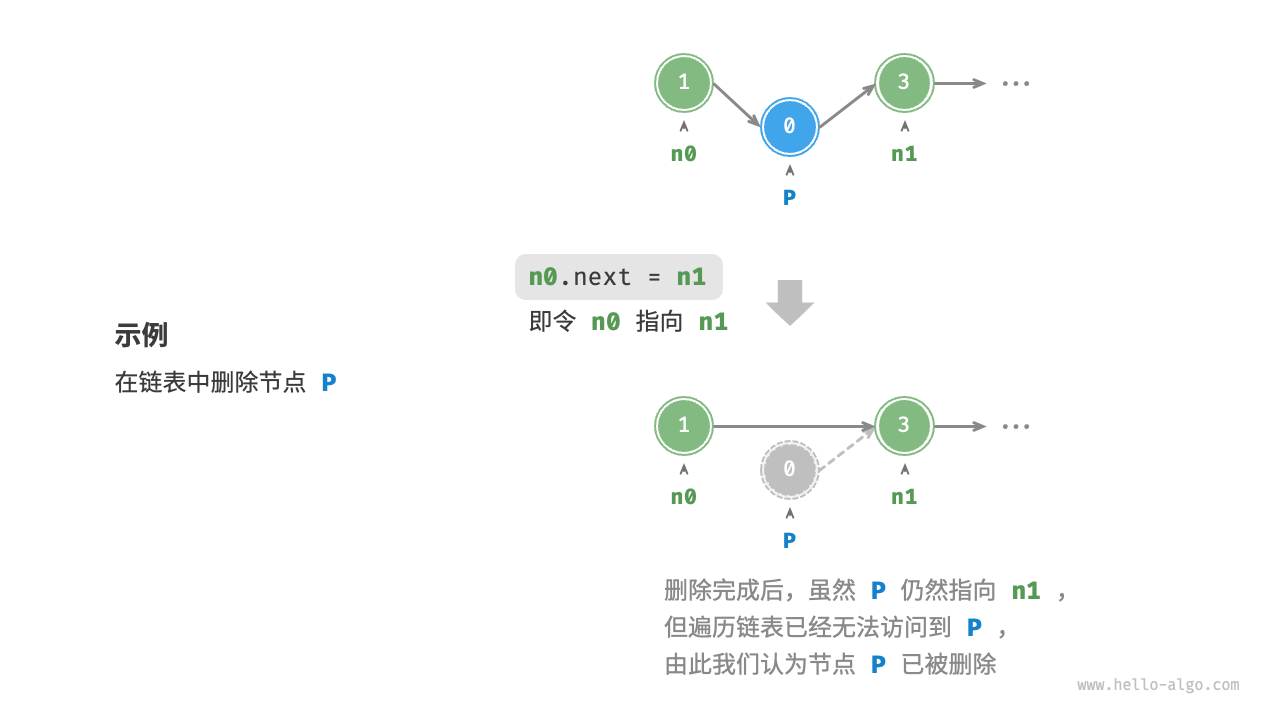
如图 4-7 所示，在链表中删除节点也非常方便，只需改变一个节点的引用（指针）即可。

请注意，尽管在删除操作完成后节点 P 仍然指向 n1 ，但实际上遍历此链表已经无法访问到 P ，这意味着 P 已经不再属于该链表了。

链表的类型

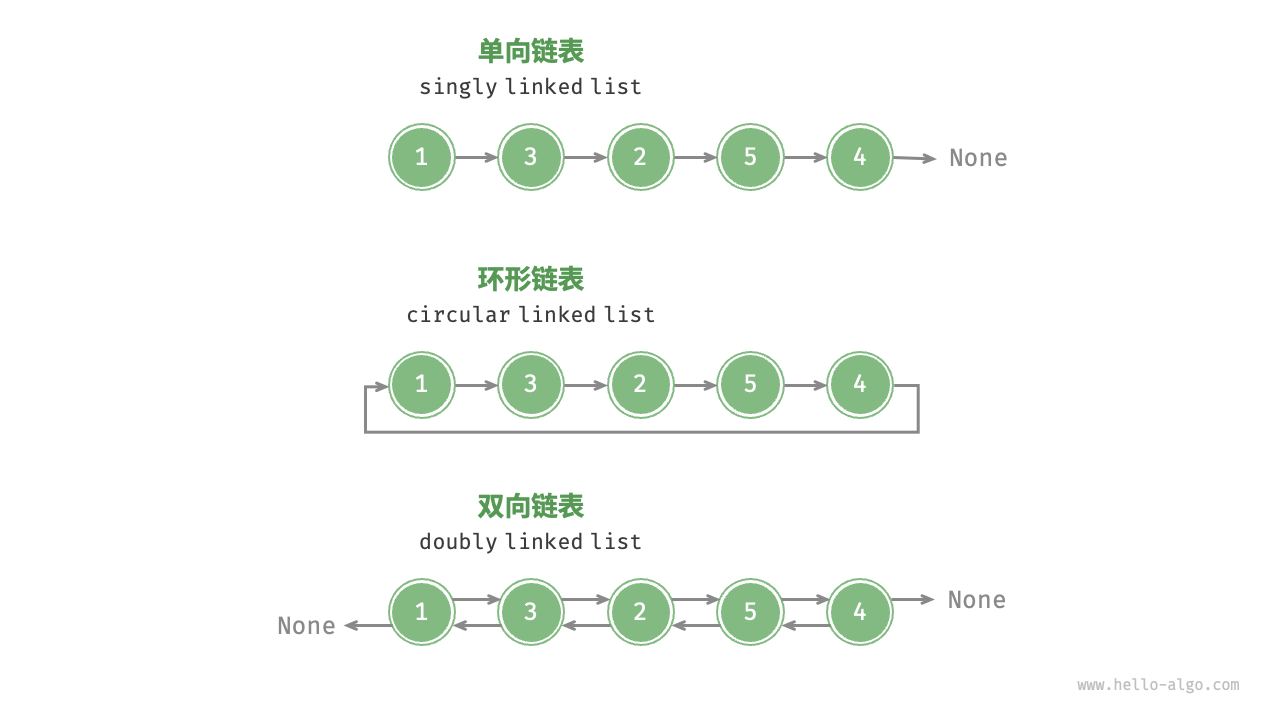
• 单向链表：即前面介绍的普通链表。单向链表的节点包含值和指向下一节点的引用两项数据。我们将首个节点称为头节点，将最后一个节点称为尾节点，尾节点指向空 None 。
• 环形链表：如果我们令单向链表的尾节点指向头节点（首尾相接），则得到一个环形链表。在环形链表中，任意节点都可以视作头节点。
• 双向链表：与单向链表相比，双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点（下一个节点）和前驱节点（上一个节点）的引用（指针）。相较于单向链表，双向链表更具灵活性，可以朝两个方向遍历链表，但相应地也需要占用更多的内存空间。

栈和队列

栈和队列也是线性表，但是是操作受限的线性表。

栈

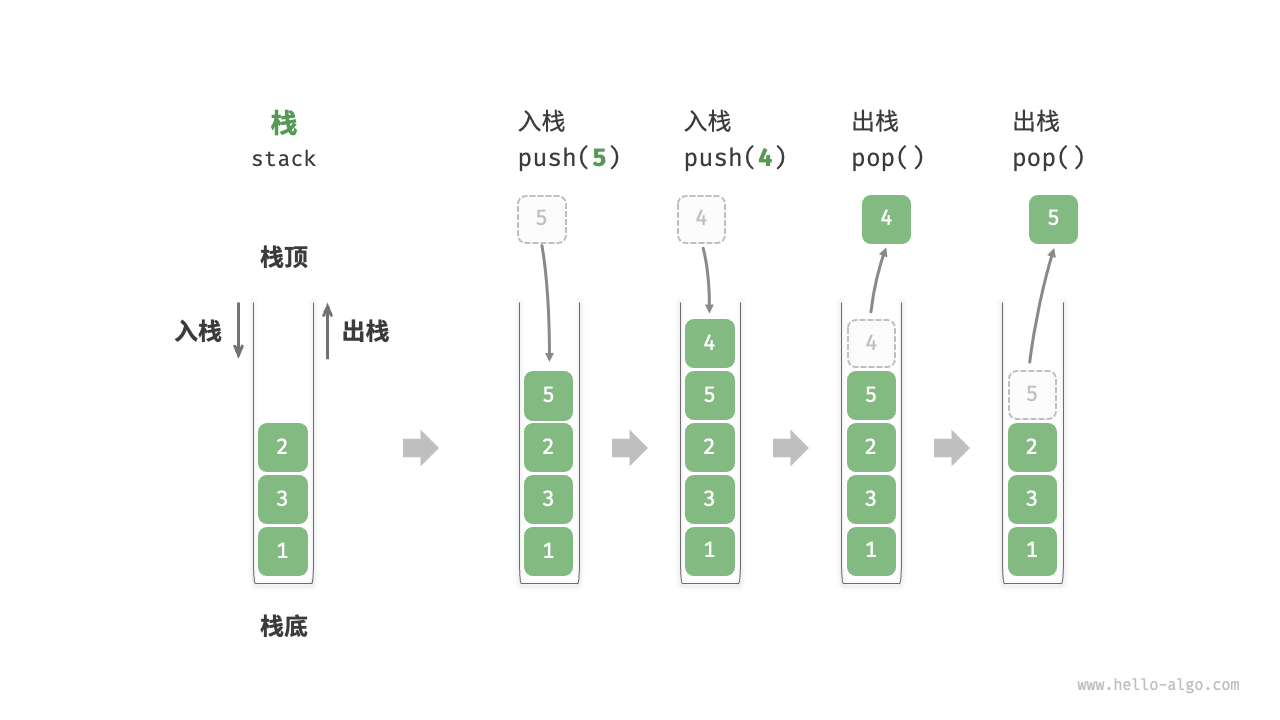
[!tip]
栈是按照“后进先出”（LIFO）的原则组织数据。栈具有记忆作用。

通常用指针top来指向栈顶的位置，用指针bottom指向栈底。
栈的存储方式可以是顺序存储，也可以是链式存储。

入栈与退栈（数组）

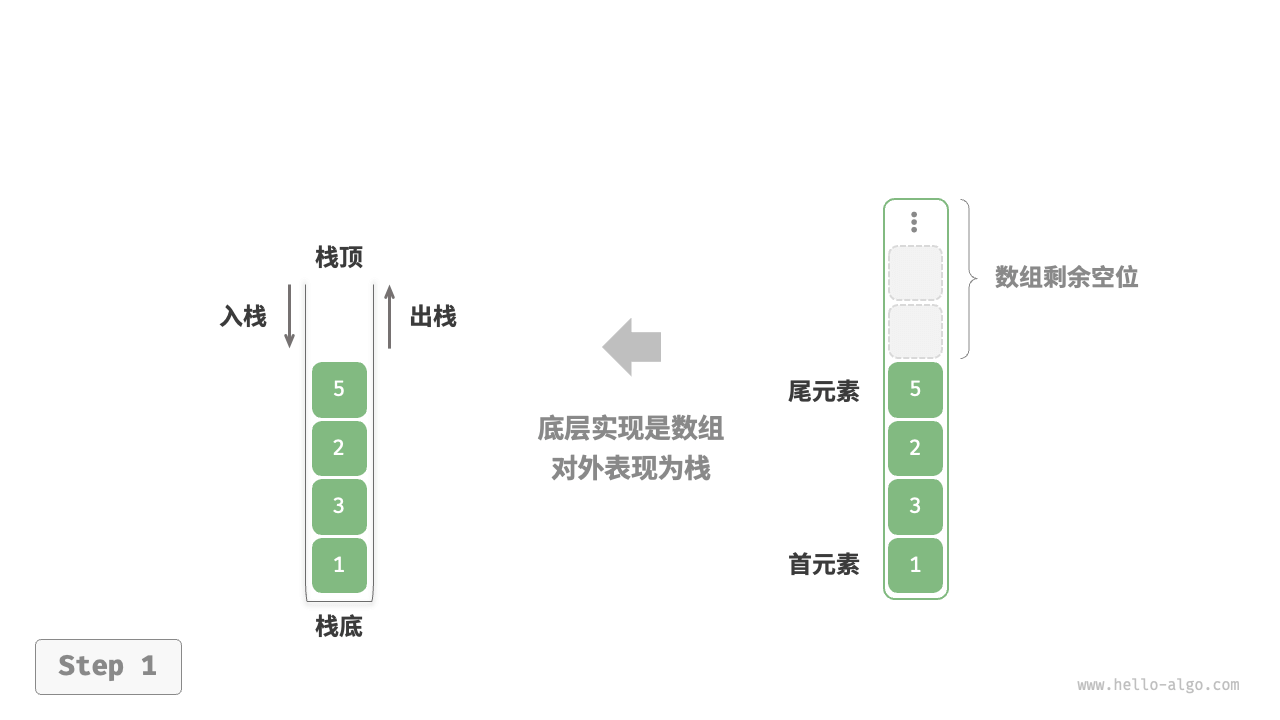
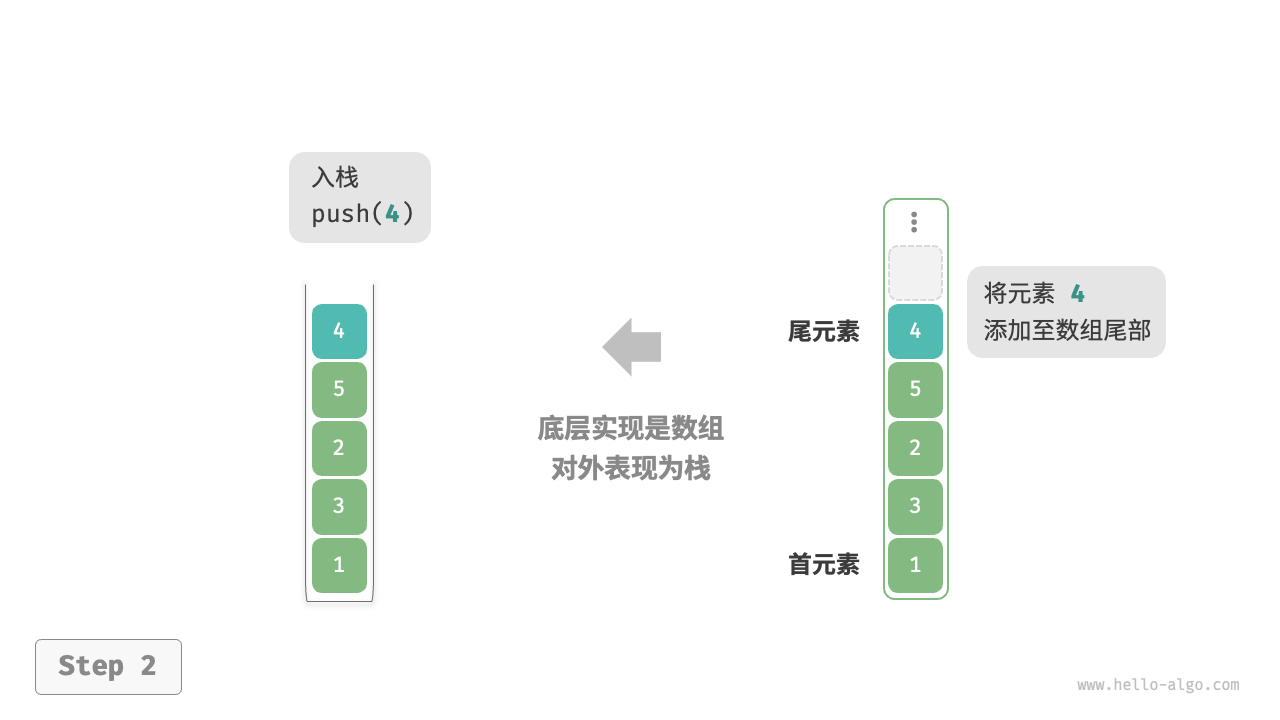
基本操作：

1. 将栈顶指针加1（即top=top+1）。
2. 将新元素插入栈顶指针指向的位置。

当栈顶指针已经指向存储空间的最后一个位置时，说明栈空间已满，不可以进行入栈操作，称为栈”上溢”错误。

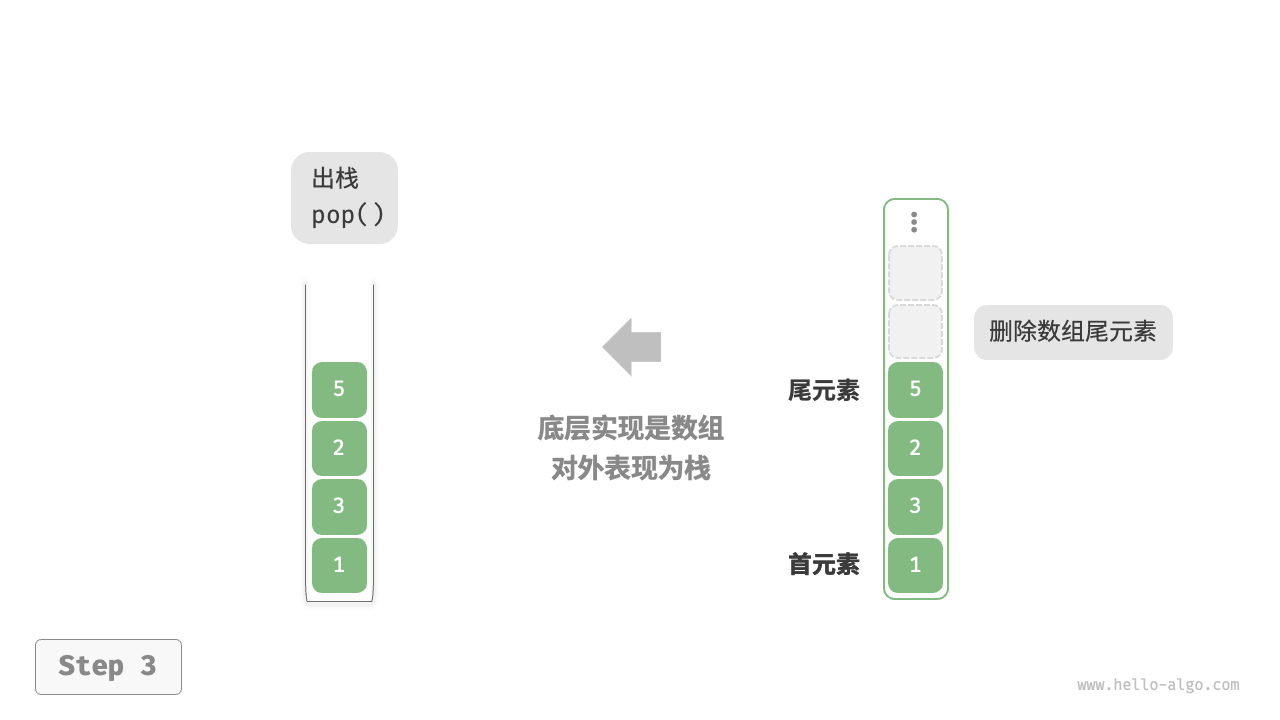
基本操作：

1. 将栈顶元素（栈顶指针指向的元素）赋给一个指定的变量。
2. 将栈顶指针减1（即top=top-1）。

当栈顶指针为0时，说明栈空，不可以进行退栈操作，称为栈”下溢”错误。

扩展：链式表

参考链接

综上所述，当入栈与出栈操作的元素是基本数据类型时，例如 int 或 double ，我们可以得出以下结论。

• 基于数组实现的栈在触发扩容时效率会降低，但由于扩容是低频操作，因此平均效率更高。
• 基于链表实现的栈可以提供更加稳定的效率表现。

扩展：典型应用

• 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页，浏览器就会对上一个网页执行入栈，这样我们就可以通过后退操作回到上一个网页。后退操作实际上是在执行出栈。如果要同时支持后退和前进，那么需要两个栈来配合实现。
• 程序内存管理。每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会不断执行出栈操作。

队列

队列（queue）是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

如图 5-4 所示，我们将队列头部称为“队首”，尾部称为“队尾”，将把元素加入队尾的操作称为“入队”，删除队首元素的操作称为“出队”。

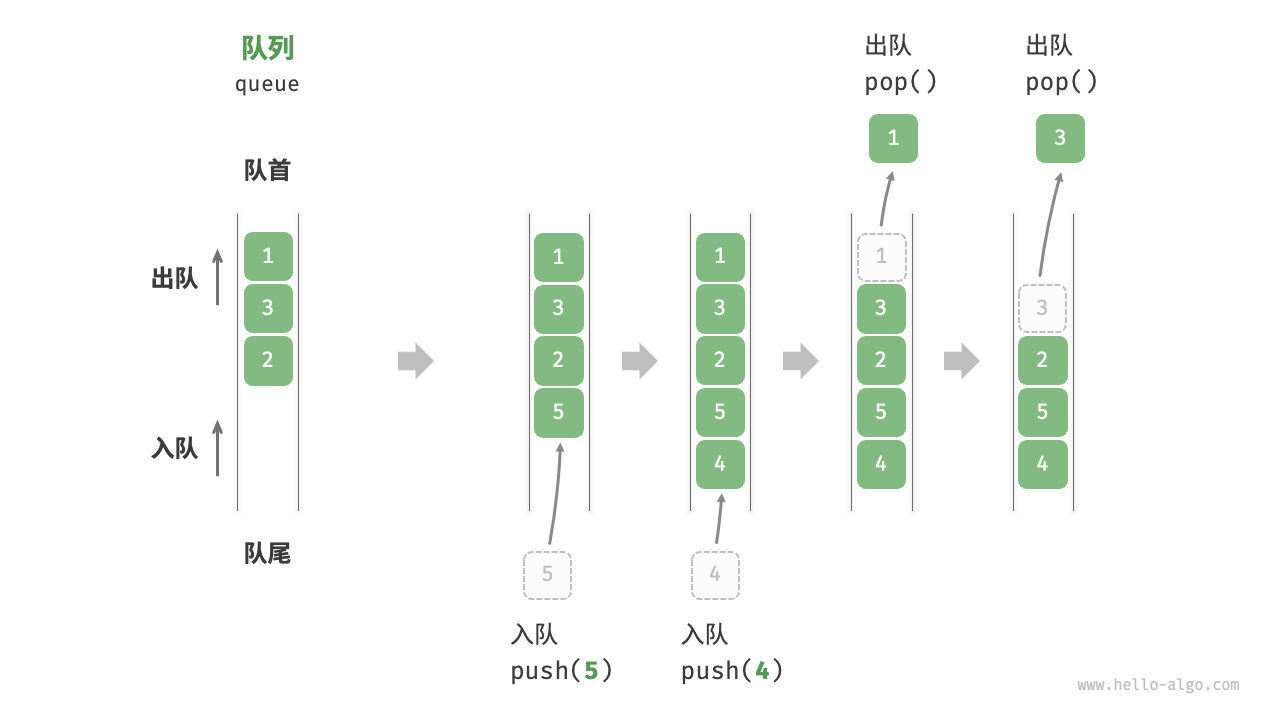
[!tip]
通常用一个指针front指向队头元素前一个位置，用指针rear指向队尾元素。

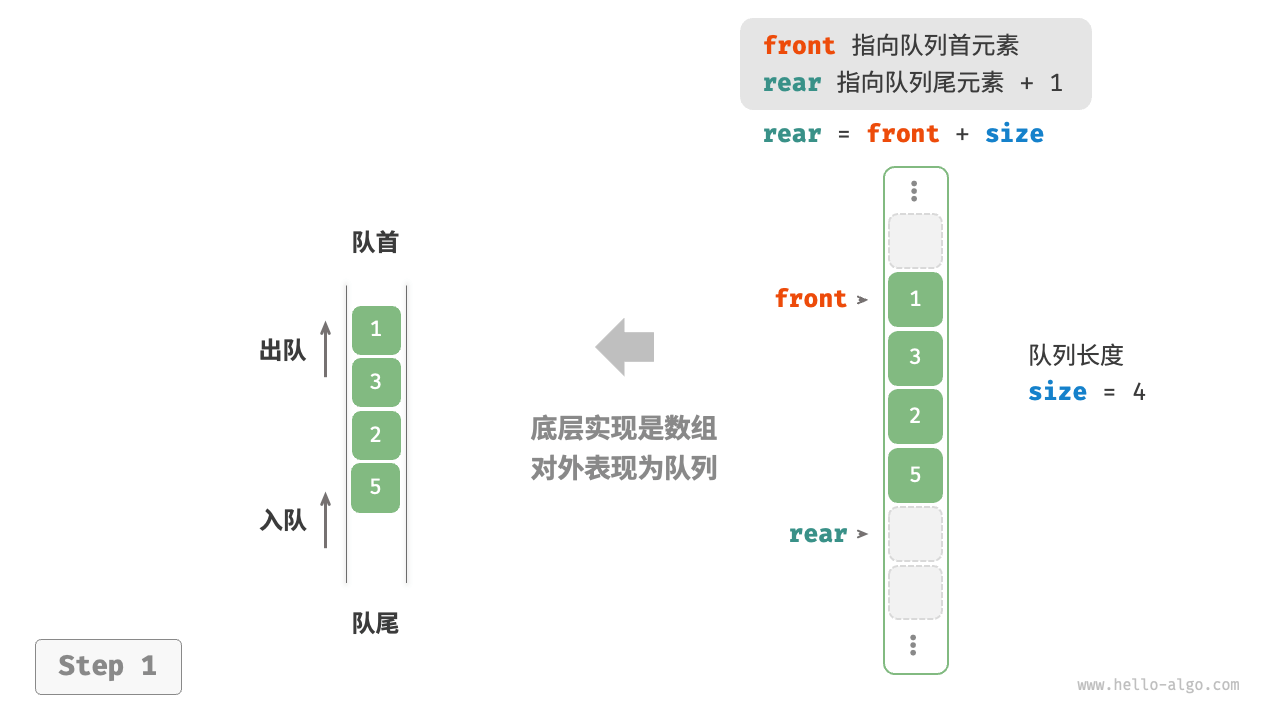
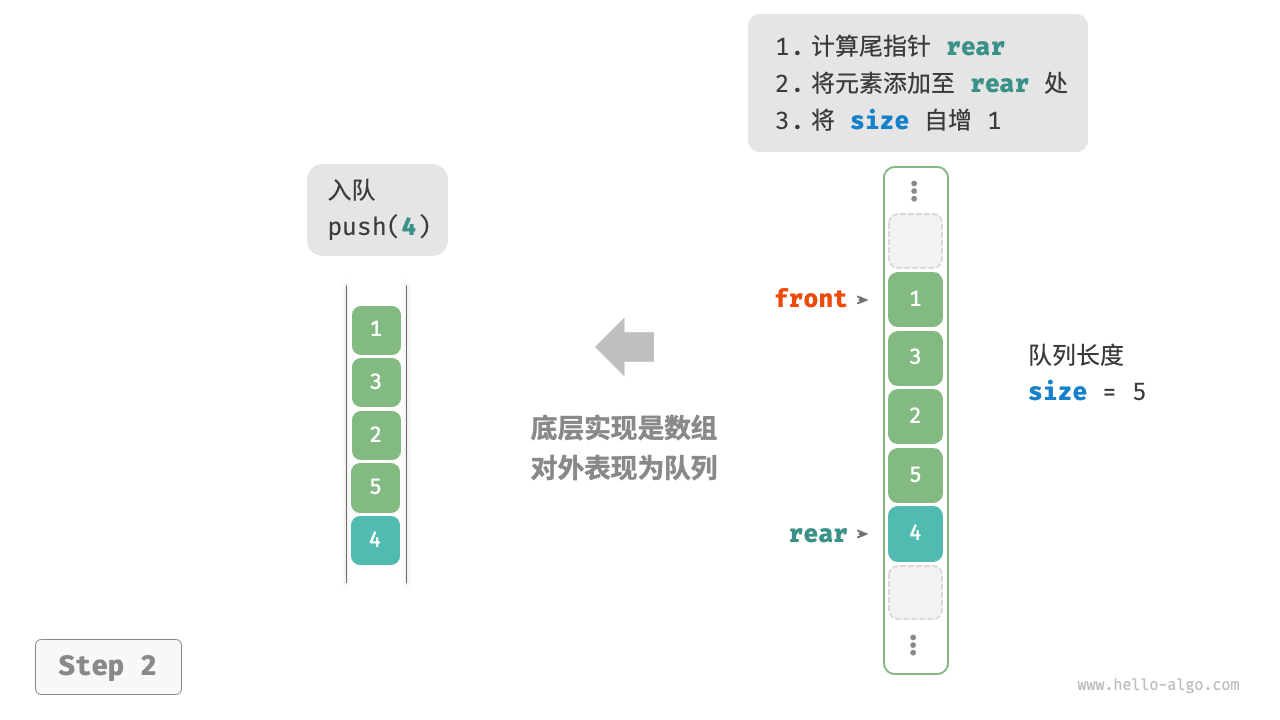
入队和出队（数组）

[!info]
此处展示的是一种效率更好的数组队列。

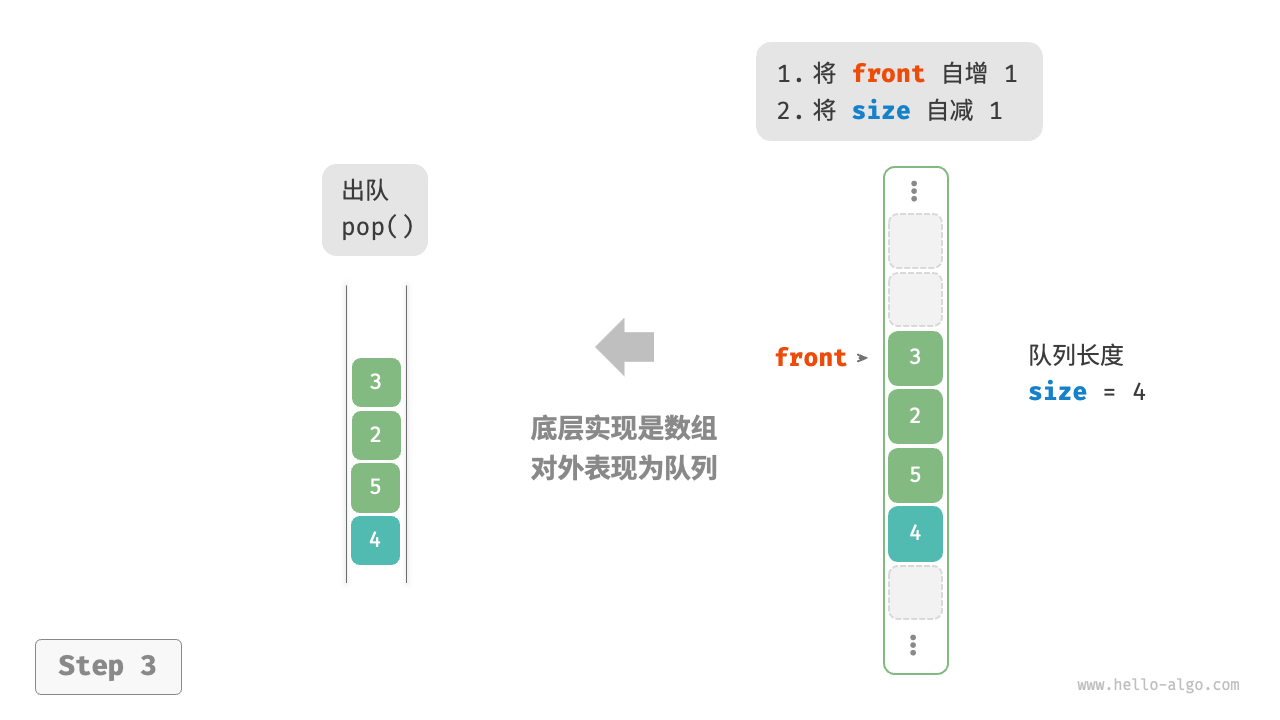
循环队列

又称“环形队列”。

[!info]
实际应用中，队列的顺序存储结构一般采用循环队列的形式。

循环队列指的是将队列存储空间的最后一个位置绕到第一个位置，形成逻辑上的环状空间，供队列循环使用。

• 在循环队列的定义中规定了两个索引指针：front 和 rear。front 指向第一个有效元素的位置，而 rear 可以理解为用来记录队尾元素的下一个位置。
• 当队列为空时，front == rear;
• 当队列满时，(rear + 1) % n = front. 这样可以让队列看起来像一个环状结构，并使得 front 和 rear 可以循环使用。
• 队列的大小为 n - 1 个元素（n-1是队列真实的容量），其中一个空位留给判断队列为空的条件。

[!warning]
注意：此处书上声明队列满时front = rear，无需留一个空位。

基本运算

假设队列的顺序存储空间的长度为m，则：

• 每进行一次入队运算，队尾指针就加1，当队尾指针rear=m+1时，则令rear=1。
• 每进行一次入队运算，队头指针就加1，当队尾指针front=m+1时，则令front=1。

图

图（graph）是一种非线性数据结构，由顶点（vertex）和边（edge）组成。我们可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。

图的常见类型与术语

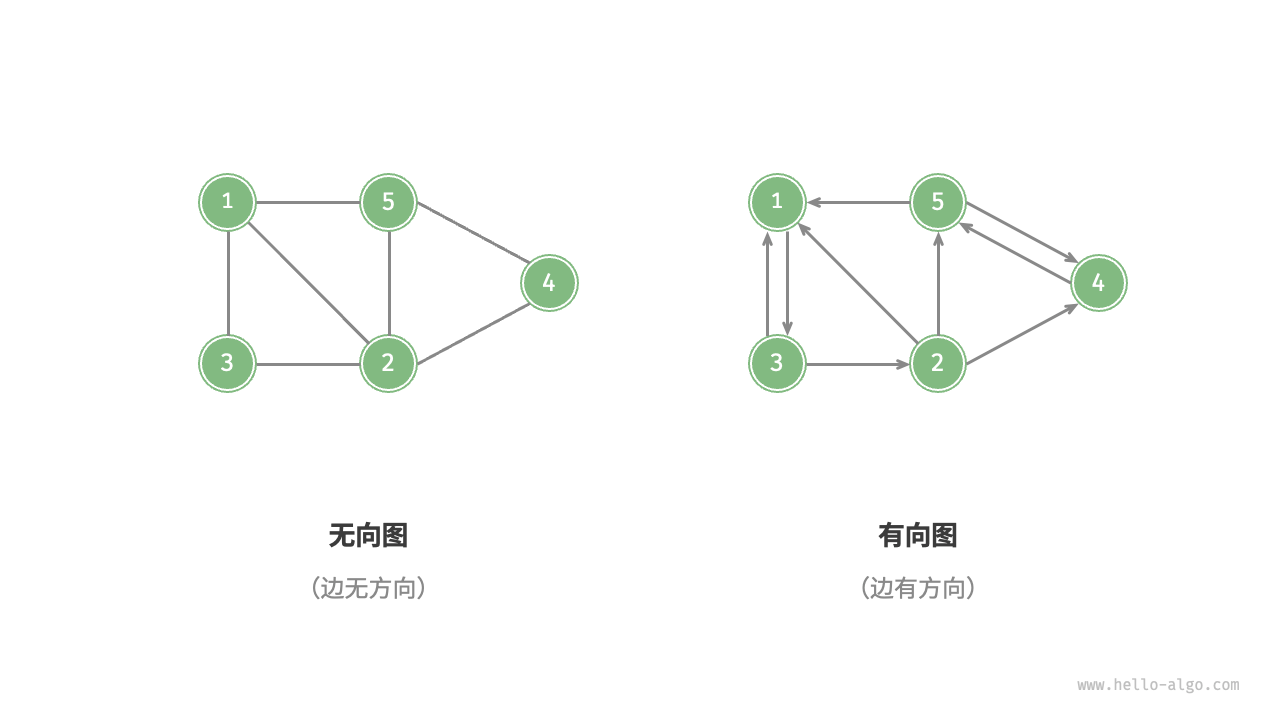
根据边是否具有方向，可分为无向图（undirected graph）和有向图（directed graph），如下图所示。

• 在无向图中，边表示两顶点之间的“双向”连接关系，例如微信或 QQ 中的“好友关系”。
• 在有向图中，边具有方向性，即 $A \rightarrow B$ 和 $A \leftarrow B$ 两个方向的边是相互独立的，例如微博或抖音上的“关注”与“被关注”关系。

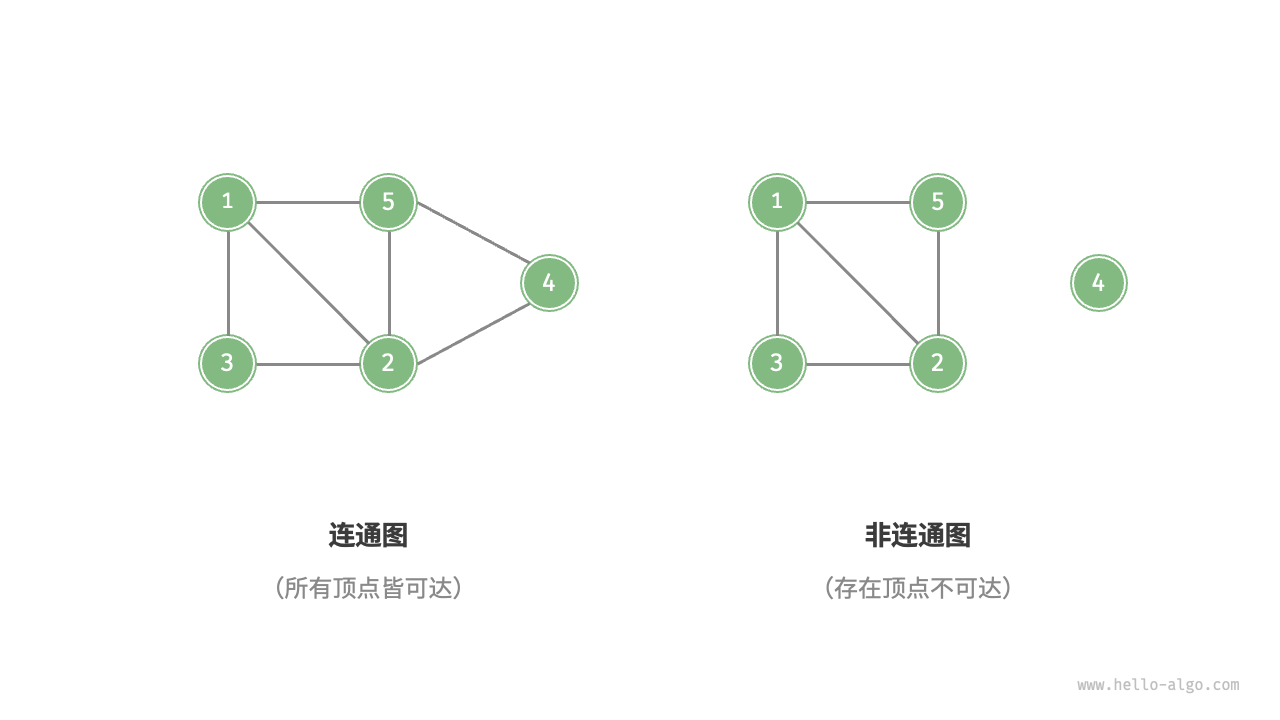
根据所有顶点是否连通，可分为连通图（connected graph）和非连通图（disconnected graph），如下图所示。

• 对于连通图，从某个顶点出发，可以到达其余任意顶点。
• 对于非连通图，从某个顶点出发，至少有一个顶点无法到达。

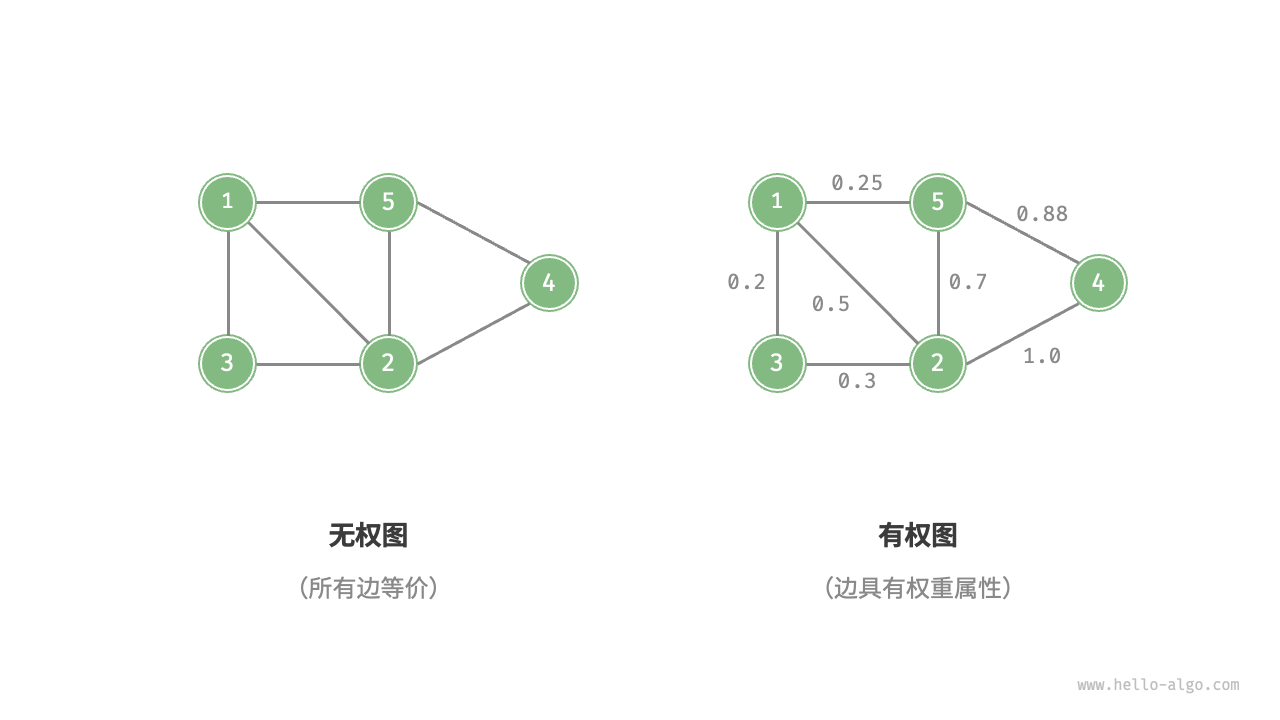
我们还可以为边添加“权重”变量，从而得到如下图所示的有权图（weighted graph）。例如在《王者荣耀》等手游中，系统会根据共同游戏时间来计算玩家之间的“亲密度”，这种亲密度网络就可以用有权图来表示。

图数据结构包含以下常用术语。

• 邻接（adjacency）：当两顶点之间存在边相连时，称这两顶点“邻接”。在上图中，顶点 1 的邻接顶点为顶点 2、3、5。
• 路径（path）：从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。在上图中，边序列 1-5-2-4 是顶点 1 到顶点 4 的一条路径。
• 度（degree）：一个顶点拥有的边数。对于有向图，入度（in-degree）表示有多少条边指向该顶点，出度（out-degree）表示有多少条边从该顶点指出。