树型结构是一类重要的非线性数据结构，其中树和二叉树是最为常用的树型结构。
树是由 n ( $n≥0$ ) 个节点组成的有限集合。

若 $n = 0$ ，称为空树。

基本性质

• 节点数等于所有节点的度数^[1]和加一。
• 度为m的树中第i层上至多有 $m^{i-1}$ 个节点。
• 高度为h的m叉树至多有$\frac{m^h-1}{m-1}$个节点。
• 具有n个节点的m叉树的最小高度为$\log_{m}{n(m-1)+1}$。

常用术语

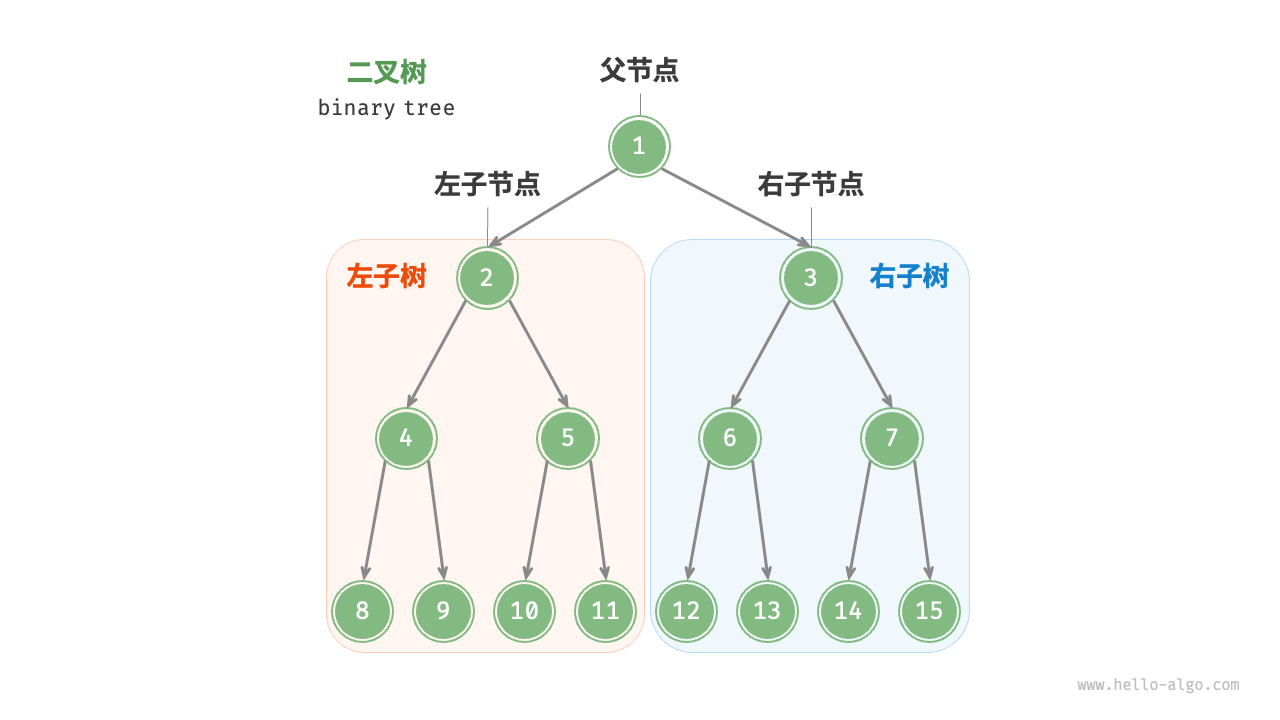
• 根节点（root node）：位于二叉树顶层的节点，没有父节点。
• 叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。
• 边（edge）：连接两个节点的线段，即节点引用（指针）。
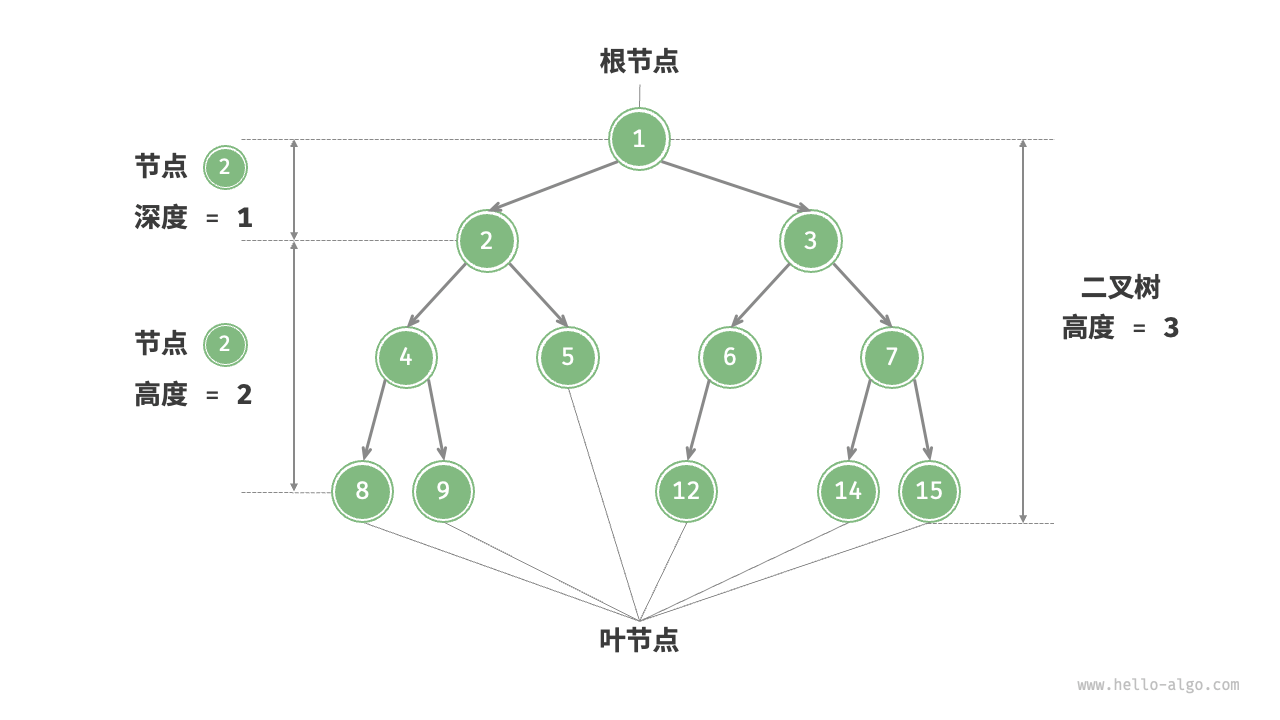
• 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。
• 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
• 二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。
• 节点的深度（depth）：从根节点到该节点所经过的边的数量。
• 节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

[!tip]
请注意，我们通常将“高度”和“深度”定义为“经过的边的数量”，但有些题目或教材可能会将其定义为“经过的节点的数量”。在这种情况下，高度和深度都需要加 1 。

本书中定义同提示中一致。以下公式均按照提示中定义表达。

二叉树

类型

满二叉树

又称"完美二叉树"。

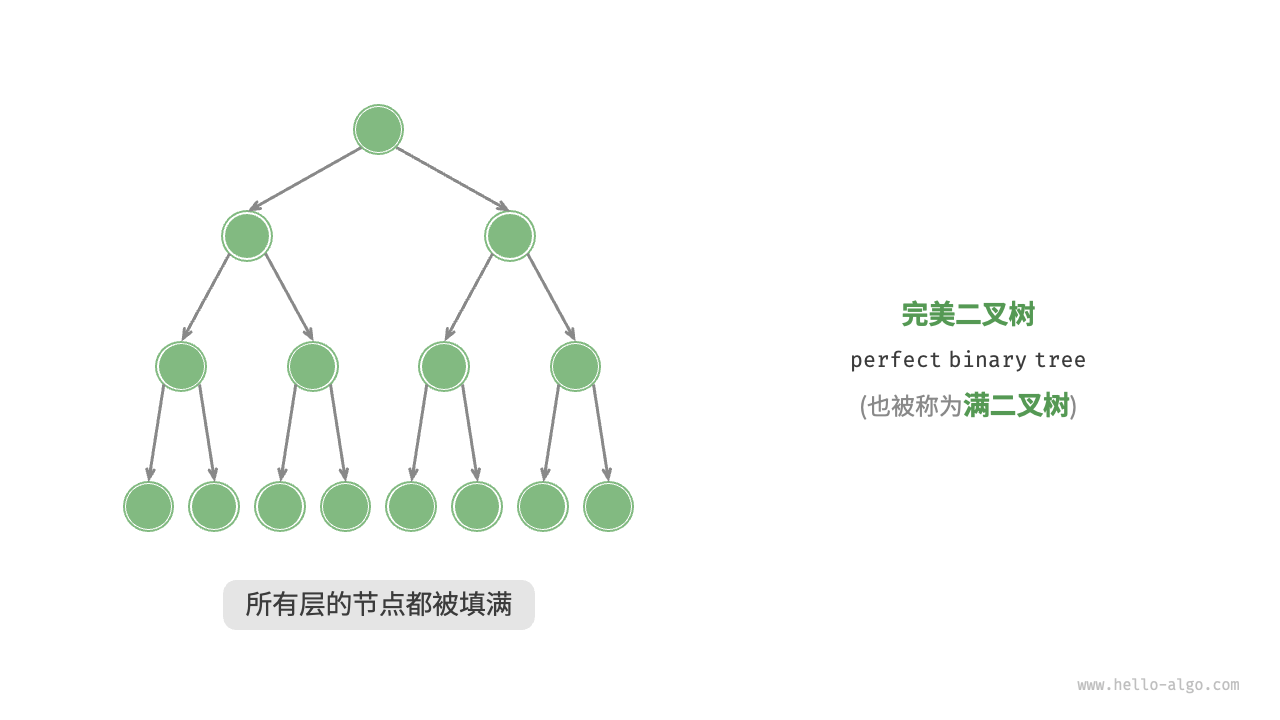
如图 7-4 所示，完美二叉树（perfect binary tree）所有层的节点都被完全填满。在完美二叉树中，叶节点的度为 0 ，其余所有节点的度都为 2 ；若树的高度（深度）为 h ，则节点总数为 $2^{h}−1$ ，呈现标准的指数级关系，反映了自然界中常见的细胞分裂现象。

完全二叉树

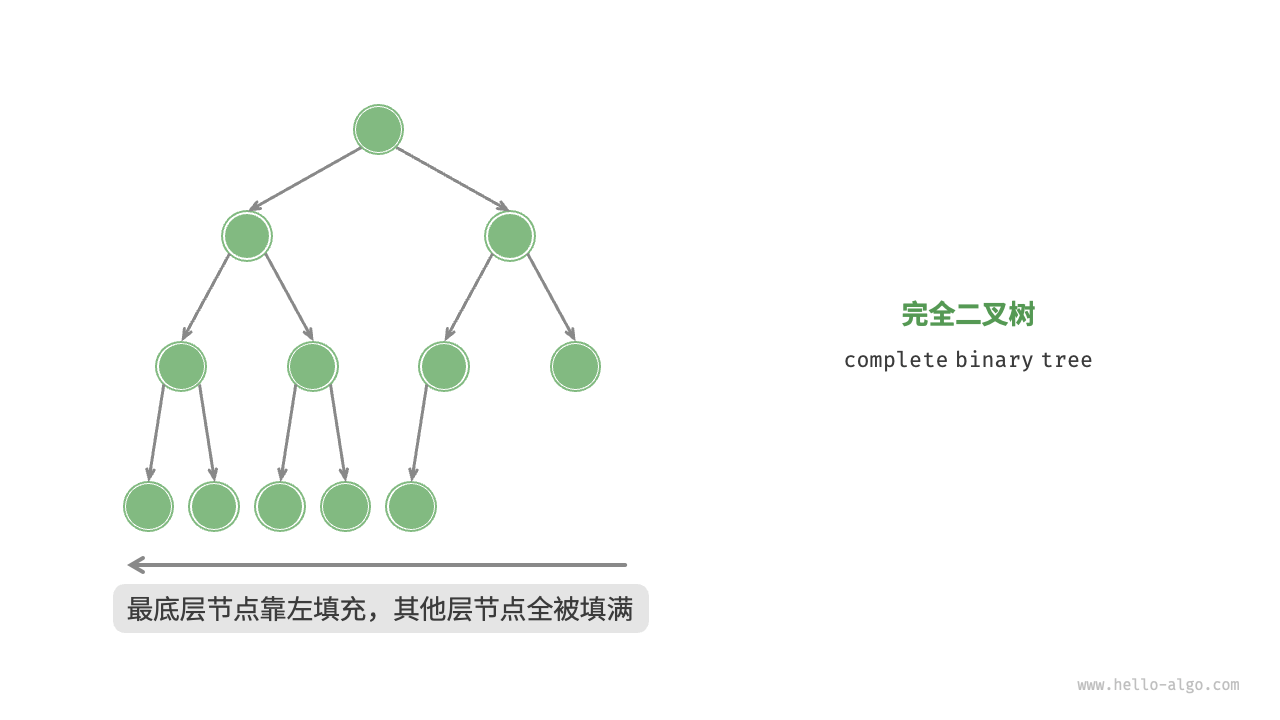
如图 7-5 所示，完全二叉树（complete binary tree）只有最底层的节点未被填满，且最底层节点尽量靠左填充。请注意，满二叉树也是一棵完全二叉树。

计算

• 若节点数量为$n$，则高度（深度）计算公式：$\left \lfloor log_{2} {n}\right \rfloor+1$

[!example]
如图 7-5 所示，本示例中有12个节点，则高度（深度）计算为

$$\left \lfloor log_{2} {12}\right \rfloor+1=\left \lfloor3.58\right \rfloor+1=3+1=4$$

我们将节点编号（从左至右，从上至下），则k节点有以下结论：

• $k=1$，该节点为根节点
• $k>1$，父节点编号为$\left \lfloor \frac{n}{2}\right \rfloor$（取整$\frac{n}{2}$）

• 若$2k\le n$，则$k$的左子节点编号为$2k$，否则该节点无左子节点、右子节点。
• 若$2k+1\le n$，则$k$的右子节点编号为$2k+1$，否则该节点无右子节点。

[!example]
如图所示，
我们假定$k=5$，则节点5的左子节点是节点10，右子节点是节点11；
假定$k=8$，均无左右子节点。

[!example] 例 5-6
一棵有 $n$ 个节点的满二叉树有多少个分支节点和多少个叶子节点？该满二叉树的高度是多少？

满二叉树中 $n_1 = 0$, 由二叉树的性质 (3) 可知 $n_0 = n_2 + 1$, 即 $n_2 = n_0 - 1$, $n = n_0 + n_1 + n_2 = 2n_0 -1$。

所以叶子节点个数 $n_0 = \frac{n+1}{2}$。分支节点个数 $n_2 = n - \frac{n+1}{2} = \frac{n-1}{2}$。

高度为 $h$ 的满二叉树的节点数 $n = 1 + 2^1 + 2^2 + ... + 2^{h-1} = 2^h - 1$, 即高度 $h = \log_2(n+1)$。

存储结构

通常采用链式存储结构，因此存储节点也由两部分组成：数据域、指针域。

由于顺序存储的空间利用率较低，因此二叉树一般都采用链式存储结构，用链表结点来存储二叉树中的每个结点。在二叉树中，结点结构通常包括若干数据域和若干指针域，二叉链表至少包含3个域：数据域 data、左指针域lchild和右指针域 rchild。

若某个指针为空，则相应指针为NULL。

左指针域	数据域	右指针域
lchild	data	rchild

[!tip]
此处书上称作 Llink-Rlink 法。

遍历

按一定次序系统地访问该二叉树中的所有节点，使每个节点恰好被访问一次。

我们可以将遍历分为前序、中序、后序遍历三种。

相应地，前序、中序和后序遍历都属于深度优先遍历（depth-first traversal），也称深度优先搜索（depth-first search, DFS），它体现了一种“先走到尽头，再回溯继续”的遍历方式。

图 7-10 展示了对二叉树进行深度优先遍历的工作原理。深度优先遍历就像是绕着整棵二叉树的外围“走”一圈，在每个节点都会遇到三个位置，分别对应前序遍历、中序遍历和后序遍历。

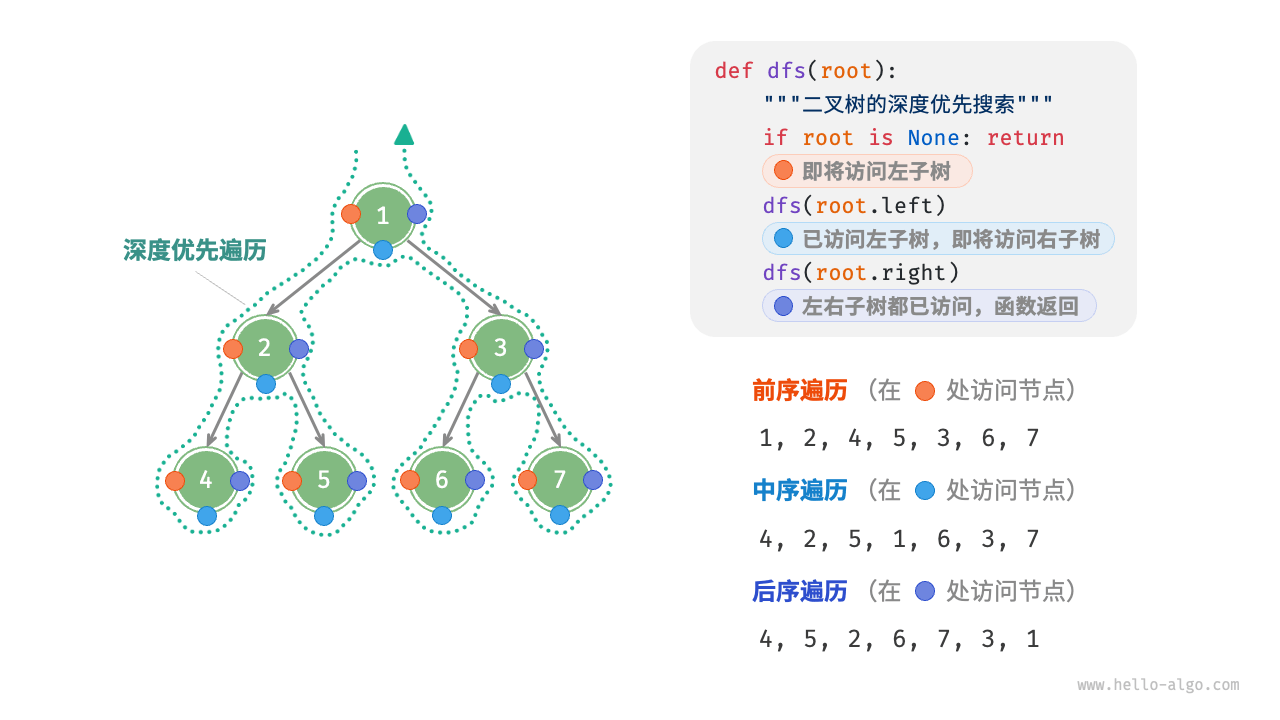
图 7-11 展示了前序遍历二叉树的递归过程，其可分为“递”和“归”两个逆向的部分。

1. “递”表示开启新方法，程序在此过程中访问下一个节点。
2. “归”表示函数返回，代表当前节点已经访问完毕。

• 时间复杂度为 $O(n)$ ：所有节点被访问一次，使用 $O(n)$ 时间。
• 空间复杂度为 $O(n)$ ：在最差情况下，即树退化为链表时，递归深度达到 $n$ ，系统占用 $O(n)$ 栈帧空间。

AI考点总结

By DeepSeek-R1

一、树的定义及性质

1. 基本概念

   • 树的定义（递归与非递归形式）
   • 术语：根、子树、父节点、子节点、兄弟节点、叶子节点、内部节点、度、层次、深度、高度
   • 树与图的区别（无环、连通性）

2. 核心性质

   • 树中节点数与边数的关系（n个节点 ⇒ n-1条边）
   • 不同树类型的性质（普通树、m叉树、森林）
   • 特殊树的特点：
     • 满二叉树：每层节点数达到最大值
     • 完全二叉树：最后一层节点左对齐，其他层填满

3. 存储结构

   • 双亲表示法（数组存储父节点索引）
   • 孩子表示法（链表存储子节点）
   • 孩子兄弟表示法（转化为二叉树结构）

4. 运算与操作

   • 树的遍历：先根遍历、后根遍历、层次遍历
   • 树的应用场景：文件系统、组织结构、决策树等

二、二叉树的构造与遍历

1. 基础性质

   • 二叉树的定义（每个节点最多两个子节点，区分左右）
   • 性质推导：
     • 第i层最多有 (2^{i-1}) 个节点
     • 深度为k的二叉树最多有 (2^k - 1) 个节点
     • 叶子节点数 (n_0) 与度为2的节点数 (n_2) 满足 (n_0 = n_2 + 1)

2. 存储结构

   • 顺序存储：完全二叉树的数组表示（父子节点下标关系）
   • 链式存储：节点结构（数据域、左/右指针）

3. 遍历方式

   • 深度优先遍历（递归与非递归实现）：
     • 先序遍历（根-左-右）
     • 中序遍历（左-根-右）
     • 后序遍历（左-右-根）
   • 广度优先遍历：层次遍历（队列实现）
   • 遍历应用：求深度、节点数、路径总和、镜像翻转等

4. 构造方法

   • 根据遍历序列构造二叉树：
     • 先序 + 中序 ⇒ 唯一二叉树
     • 后序 + 中序 ⇒ 唯一二叉树
   • 特殊二叉树的构造：
     • 完全二叉树的数组生成
     • 二叉搜索树（BST）的构造与平衡化（AVL树、红黑树基础概念）
     • 堆的构造（最大堆/最小堆）

5. 特殊二叉树

   • 二叉搜索树（BST）：定义、查找、插入、删除操作（含删除后的调整）
   • 平衡二叉树：AVL树的旋转操作（左旋、右旋）
   • 堆：插入（上浮）、删除（下沉）、堆排序原理
   • 哈夫曼树：构造过程、带权路径长度计算、编码应用

6. 高级操作与算法

   • 判断二叉树的性质：是否对称、平衡、完全二叉树
   • 二叉树与树的转换：孩子兄弟表示法
   • 二叉树序列化与反序列化（如JSON格式）
   • 常见算法题：最近公共祖先（LCA）、直径计算、路径总和、子树判断

三、高频考点总结

1. 树与二叉树的区别：二叉树严格区分左右，普通树不区分。
2. 完全二叉树的判断：层次遍历检查是否存在空缺节点。
3. 非递归遍历：栈模拟递归（先序/中序/后序）、队列层次遍历。
4. 线索二叉树：利用空指针线索化，优化遍历效率。
5. 应用场景：表达式树求值、哈夫曼编码压缩、堆实现优先队列。